統計〜児童が解決したくなる題材で，PPDACサイクルを意識した展開に
新学習指導要領では，「Ｄデータの活用」領域が新設され，6年間を通して統計的に問題解決する力を
高めていくことになります。
児童が興味をもって解決したくなる題材を
選定しました。
選定しました。
▼2年上「グラフと ひょう」p.8
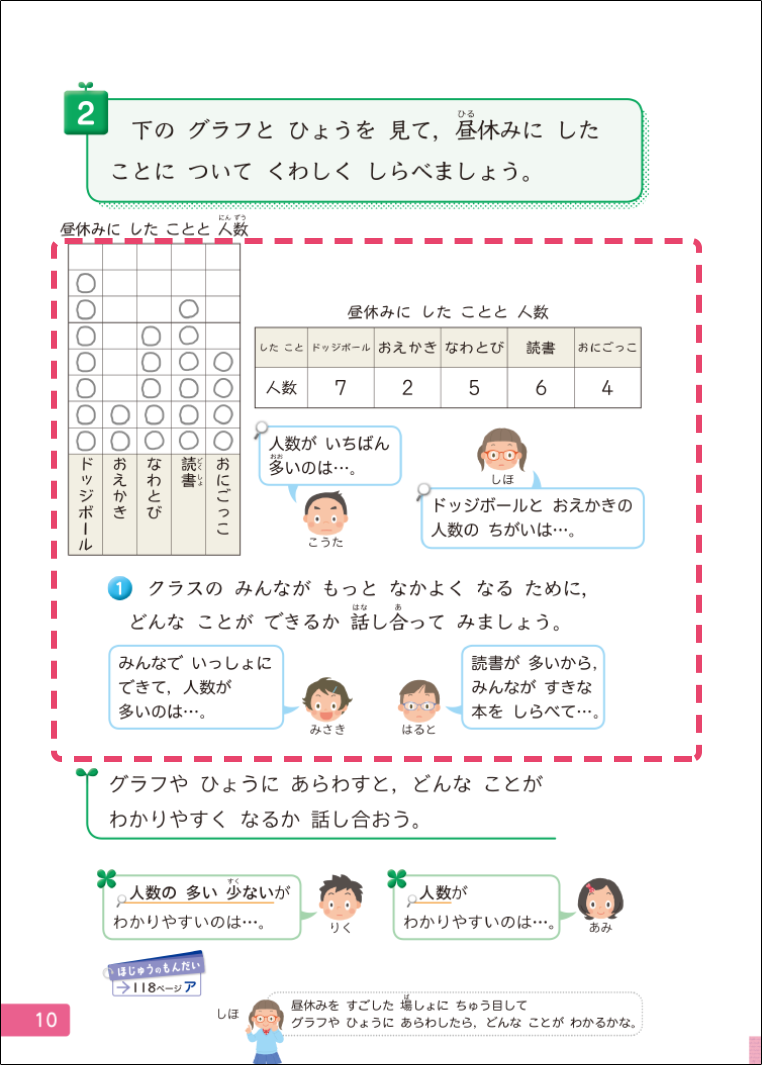
▼2年上「グラフと ひょう」p.10
５，６年では，単元の学習の後に，
統計的な問題解決の方法（PPDACサイクル）を
振り返るページを新設しました。
統計的な問題解決の方法（PPDACサイクル）を
振り返るページを新設しました。
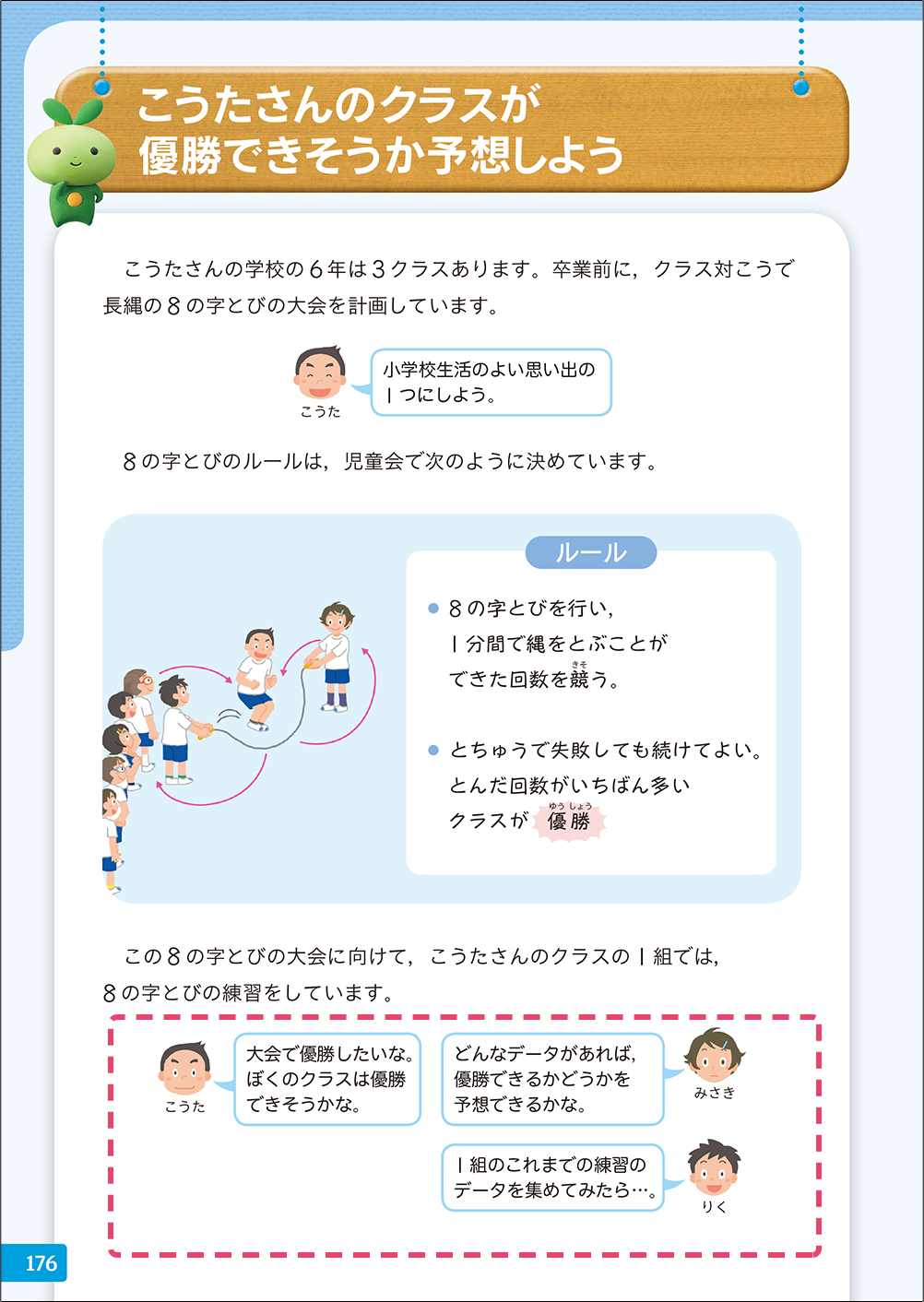
▼6年「データの調べ方」p.176
▼6年「データの調べ方」p.180~181
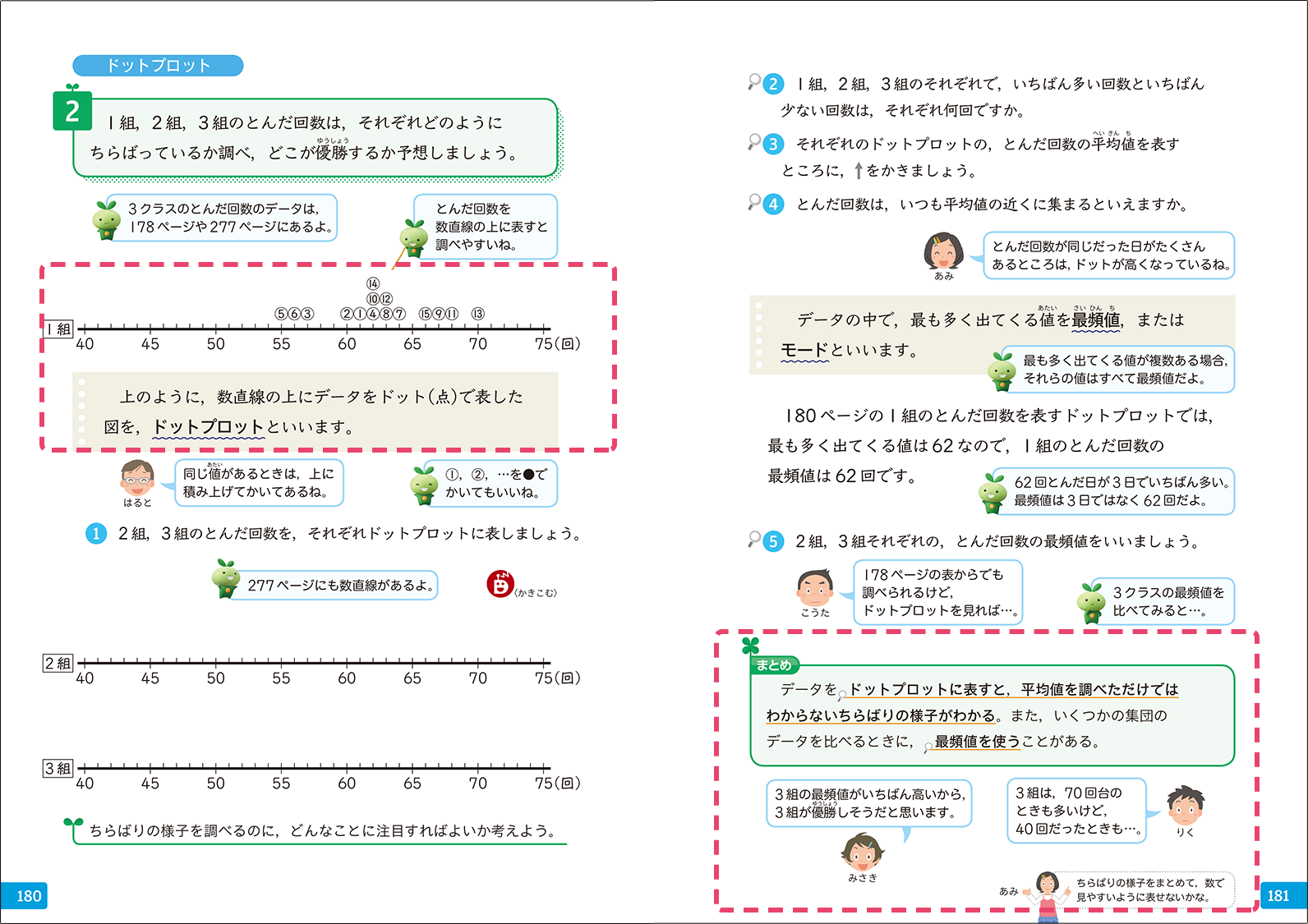
▼6年「データの調べ方」p.188
▼6年「データの調べ方」p.189
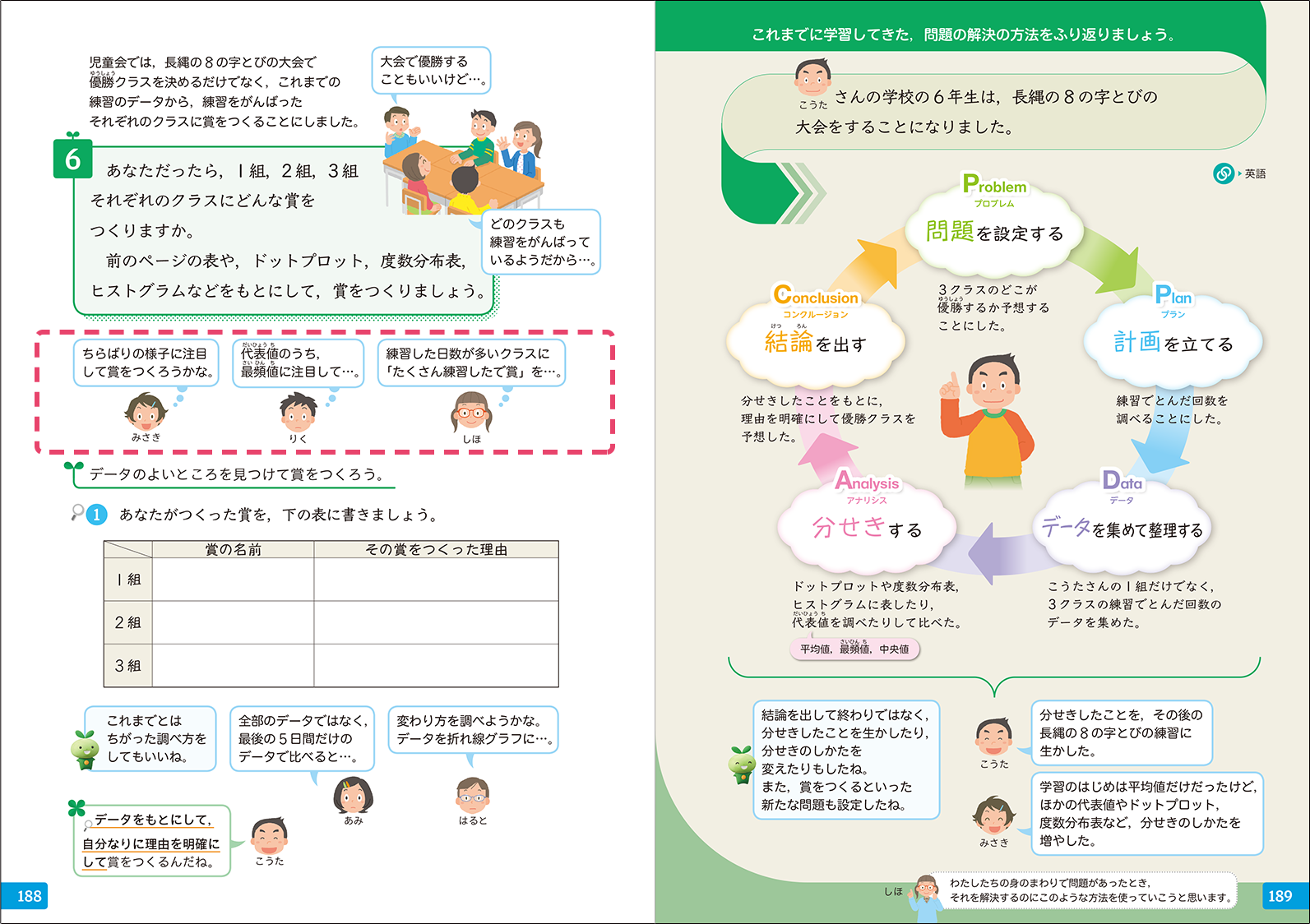
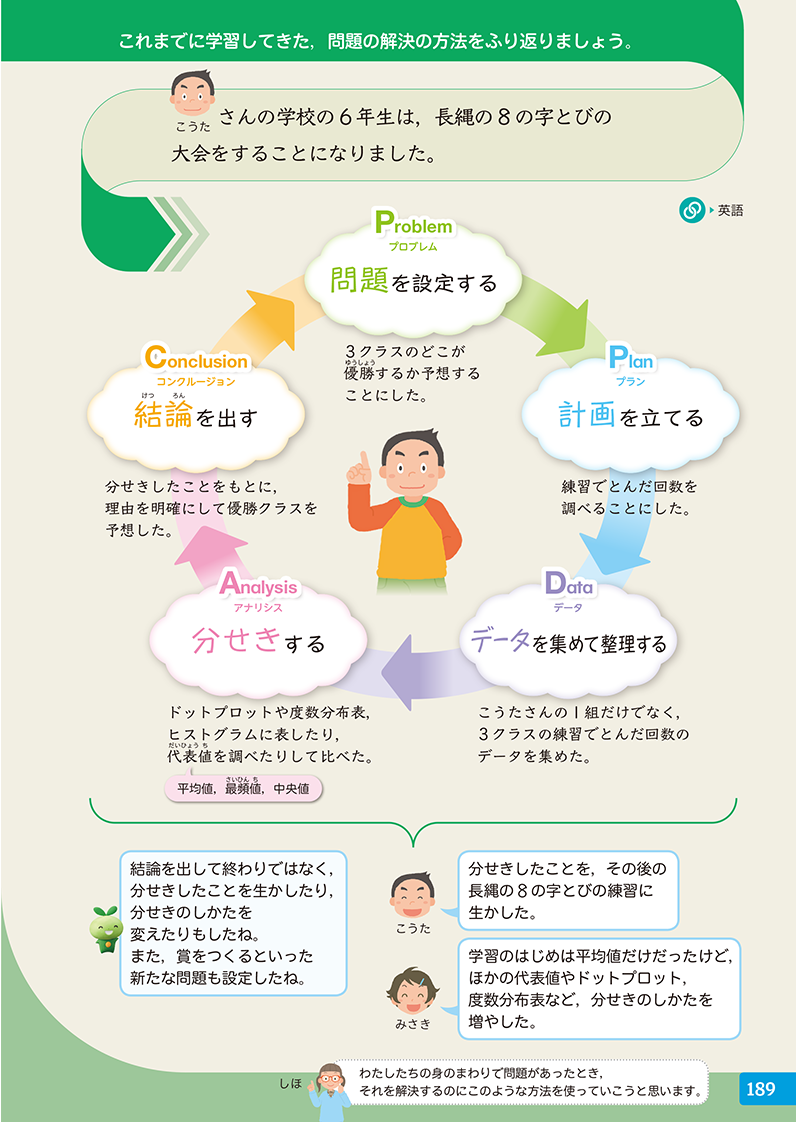
▼6年「データの調べ方」p.193
倍と割合〜下学年から，割合に関する学習をていねいに積み上げる
新学習指導要領では，４年に「簡単な場合についての割合」が新しく位置付けられ，下学年からの学習の
積み上げがいっそう大切になります。
３年以降は，
倍に関する内容を単元化して，三用法をセットで扱うようにしました。
常に三用法を相互に関連付けてとらえることで，倍についての理解を深めます。
倍に関する内容を単元化して，三用法をセットで扱うようにしました。
常に三用法を相互に関連付けてとらえることで，倍についての理解を深めます。
▼3年下「倍の計算」p.73
４年の「簡単な場合についての割合」では，
連続量で均質性を仮定しやすい包帯の伸び方を比較する問題を採用しました。
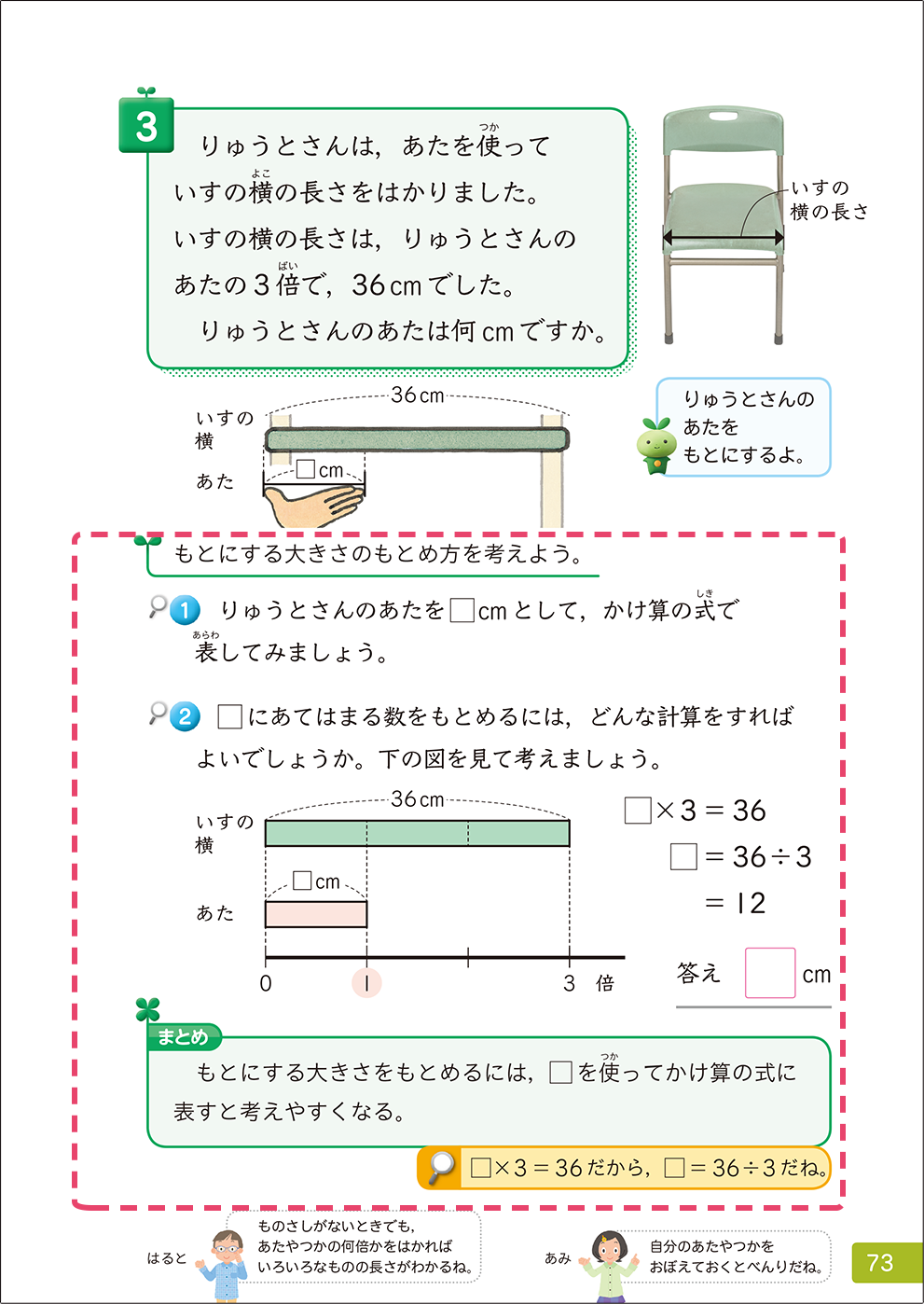
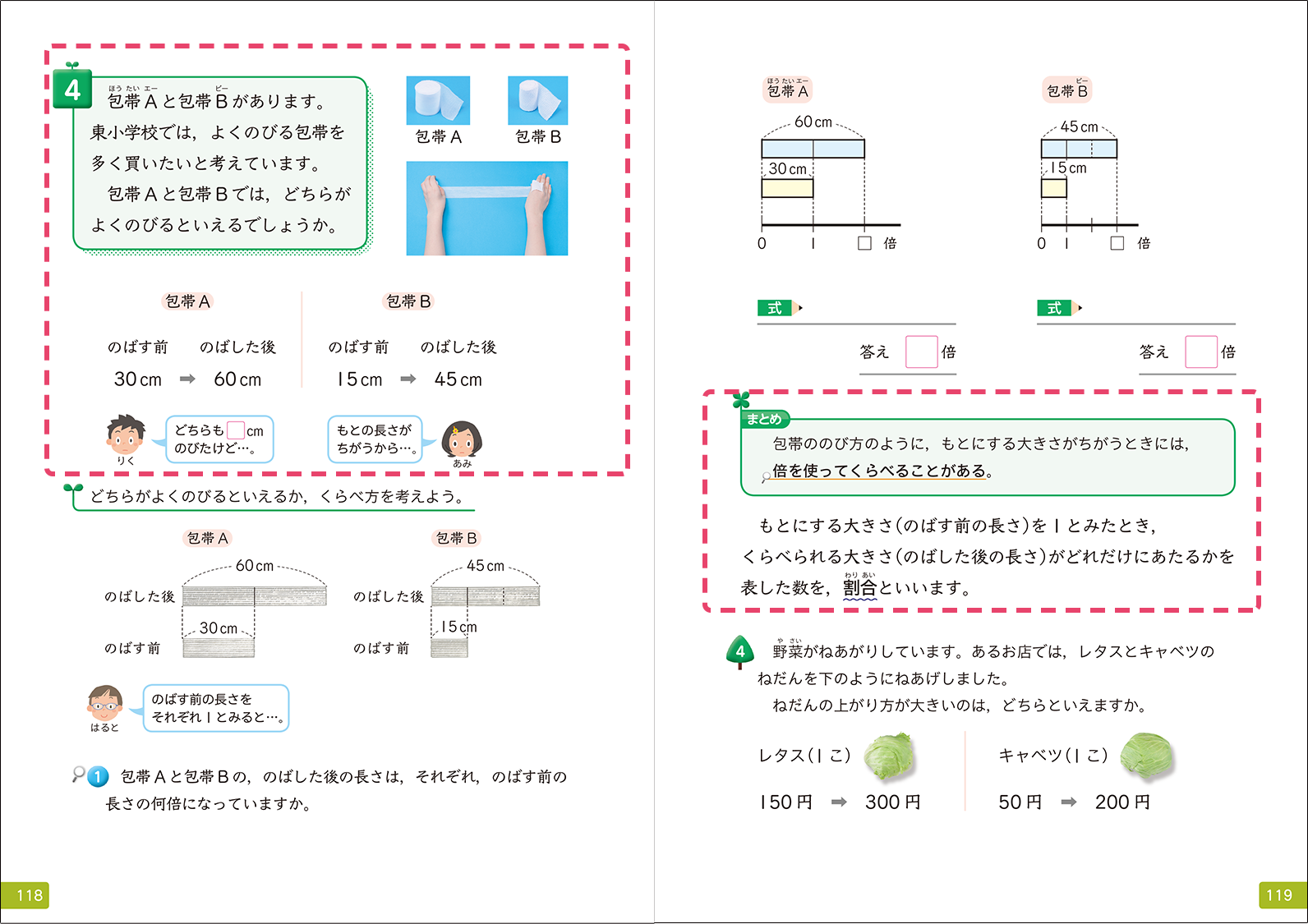
連続量で均質性を仮定しやすい包帯の伸び方を比較する問題を採用しました。
▼4年上「倍の見方」p.118-119
「１とみると〇にあたる」という倍の意味は
高学年になっても理解が難しいです。
高学年になっても理解が難しいです。
「１とみると〇にあたる」という倍の意味は，
ことばだけでなく，
数直線を活用した理解を重視しました。
ことばだけでなく，
数直線を活用した理解を重視しました。
▼4年上「倍の見方」p.114-115
▼5年上「小数の倍」p.65
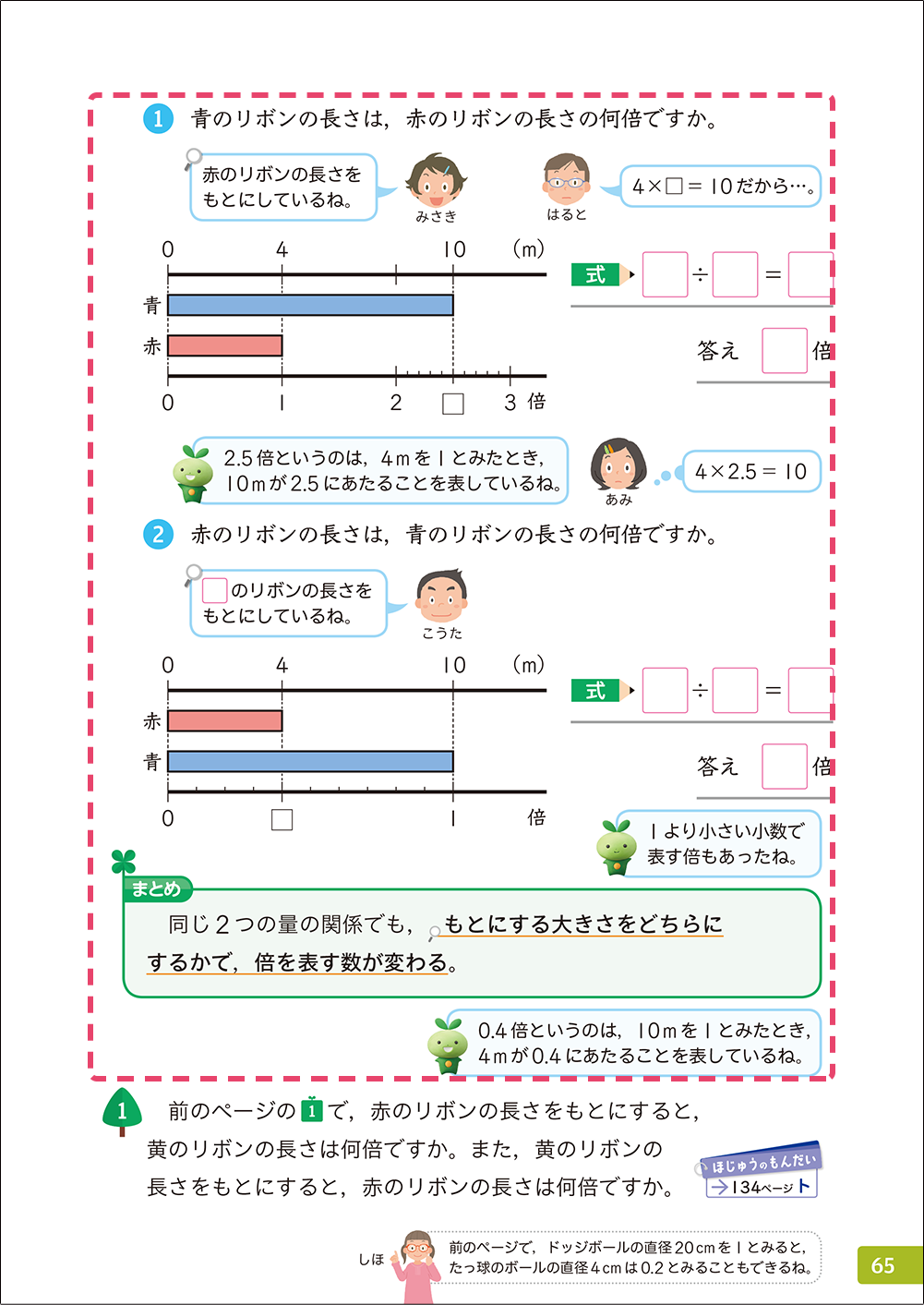
5年では，学力調査で正答率の低かった割合の問題も，教材化して取り扱っています。
別紙パンフレット「つまずきへの取り組み」（p.5）もご覧ください。
分数〜分数の学習を通して，割合の素地をつくる
新学習指導要領では，２年の分数「
, 
など簡単な分数について…」が「 , 
など簡単な分数に
ついて…」に変更されました。
になったことにより，割合との関連をいっそう意識した指導が重要になります。
2年「分数」で，
倍の学習と分数を関連付ける
ページを新設しました。
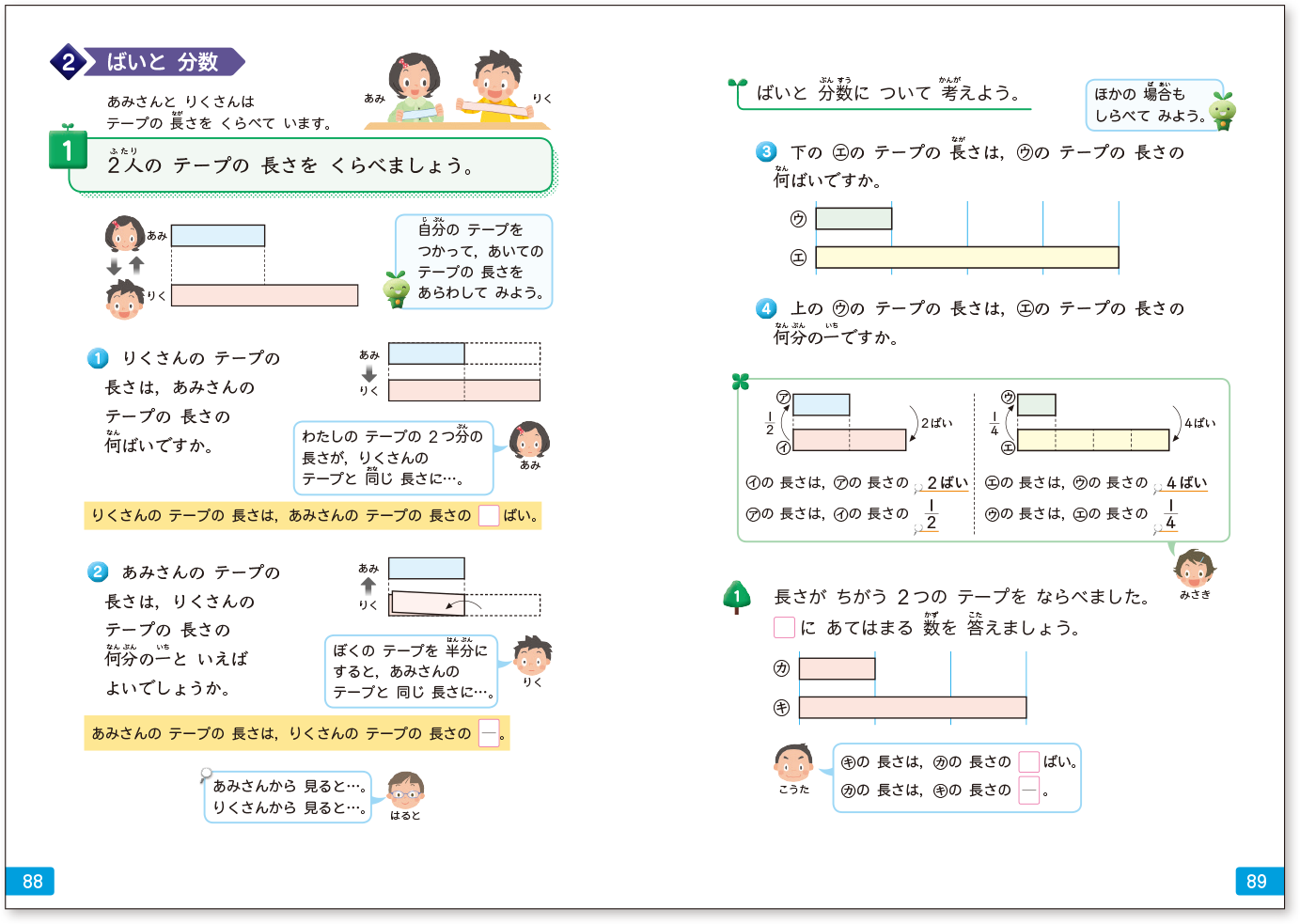
倍の学習と分数を関連付ける
ページを新設しました。
▼2年下「分数」p.88-89
３年では，等分除の場面と分数を関連付けるページを新設しました。
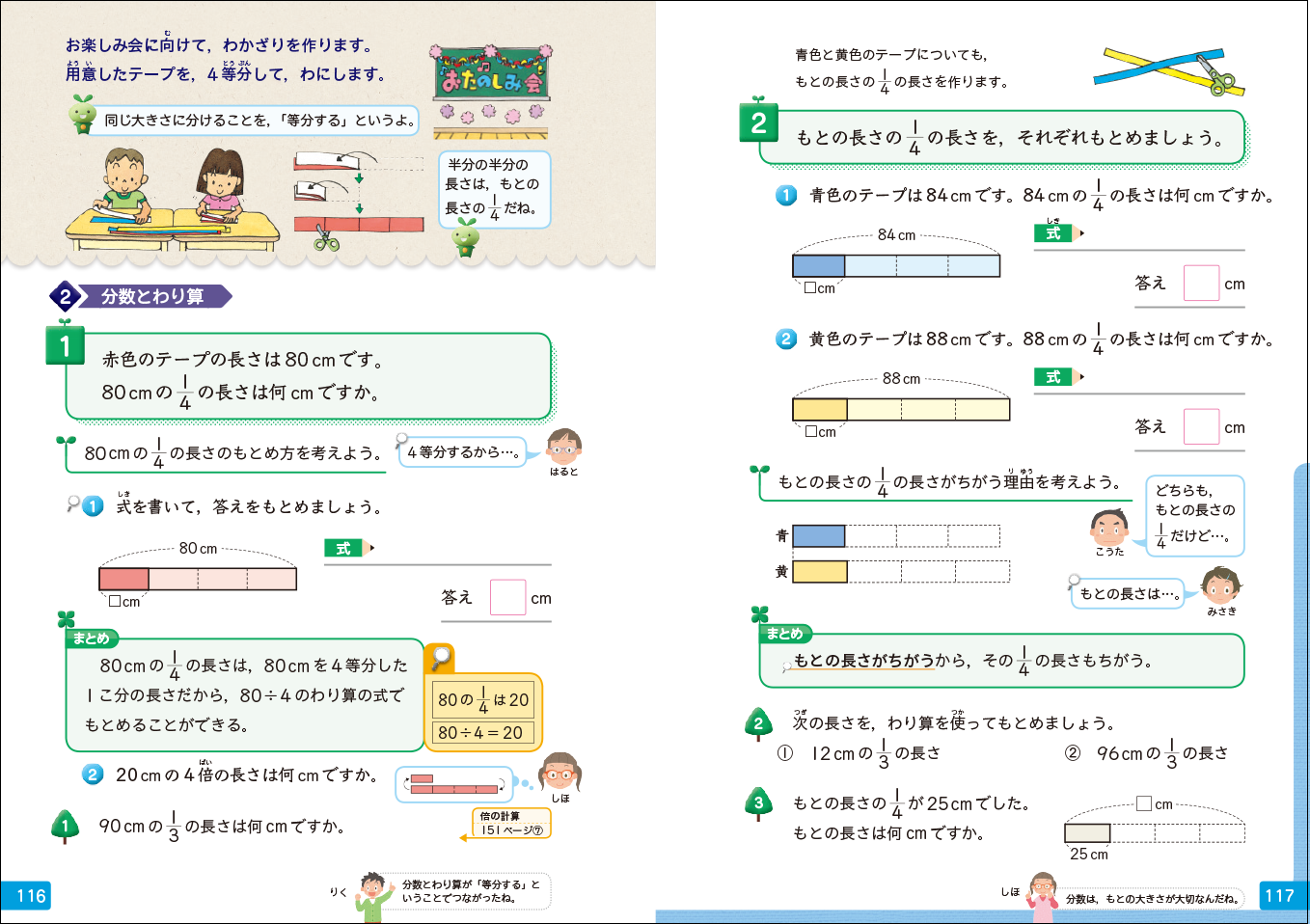
▲３年上「大きい数のわり算，分数とわり算」p.116-117
3年以降の学習でも，分数と割合を関連付けて取り扱いました。
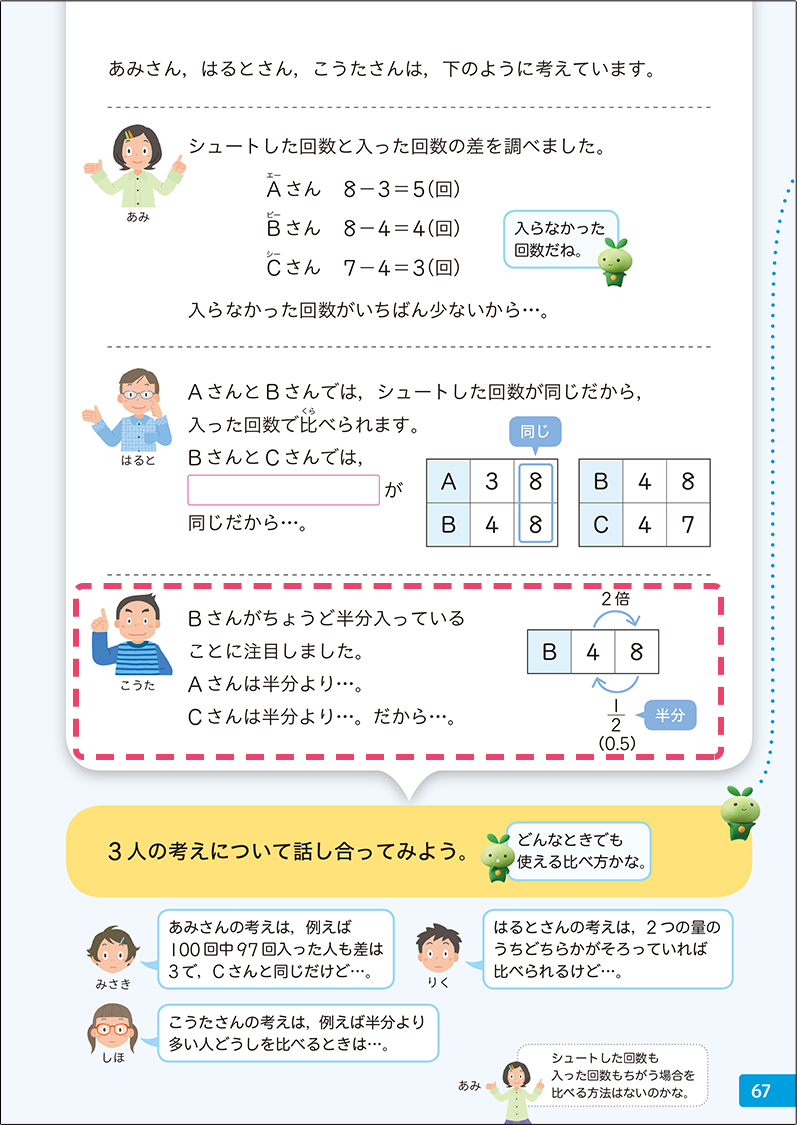
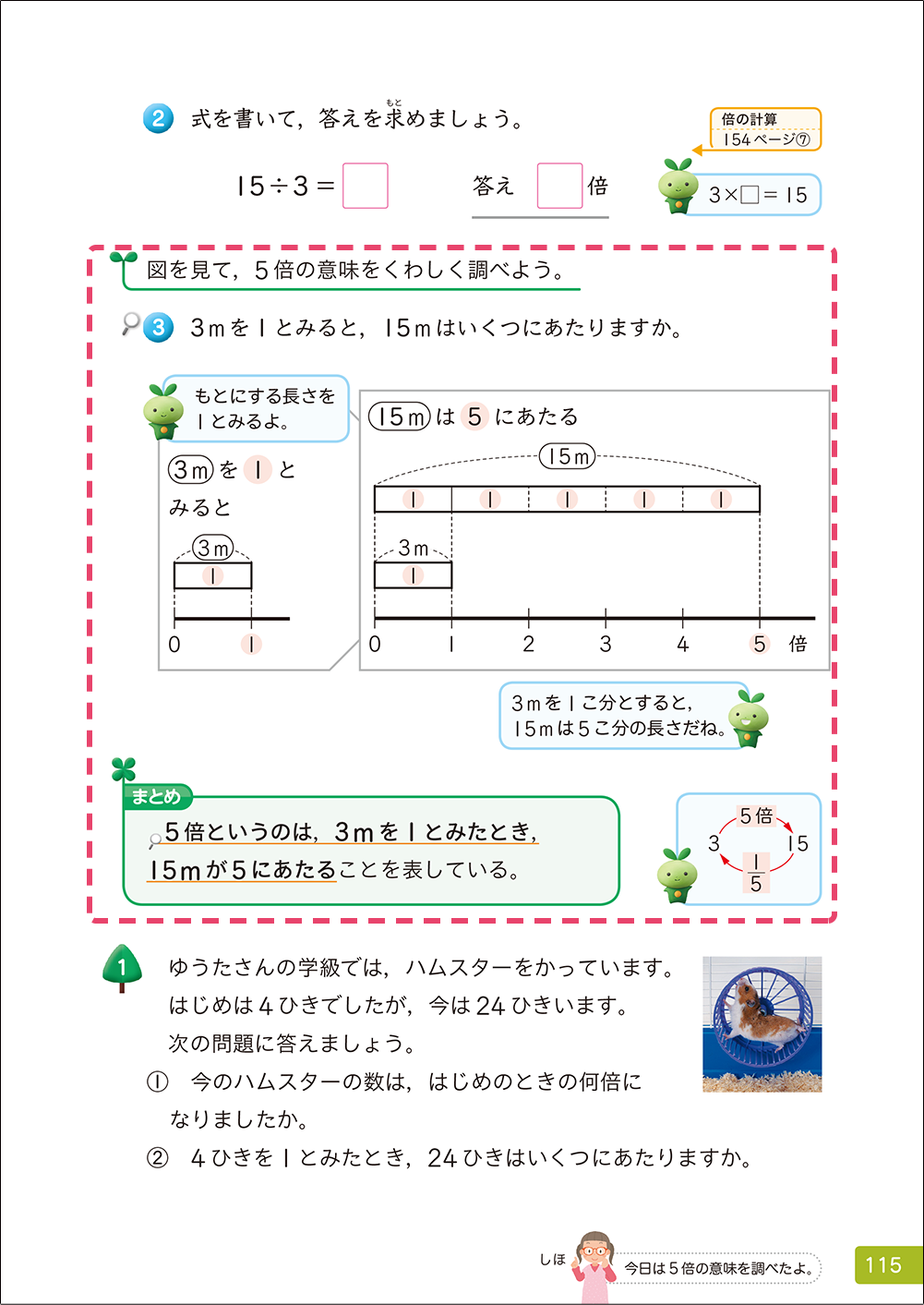
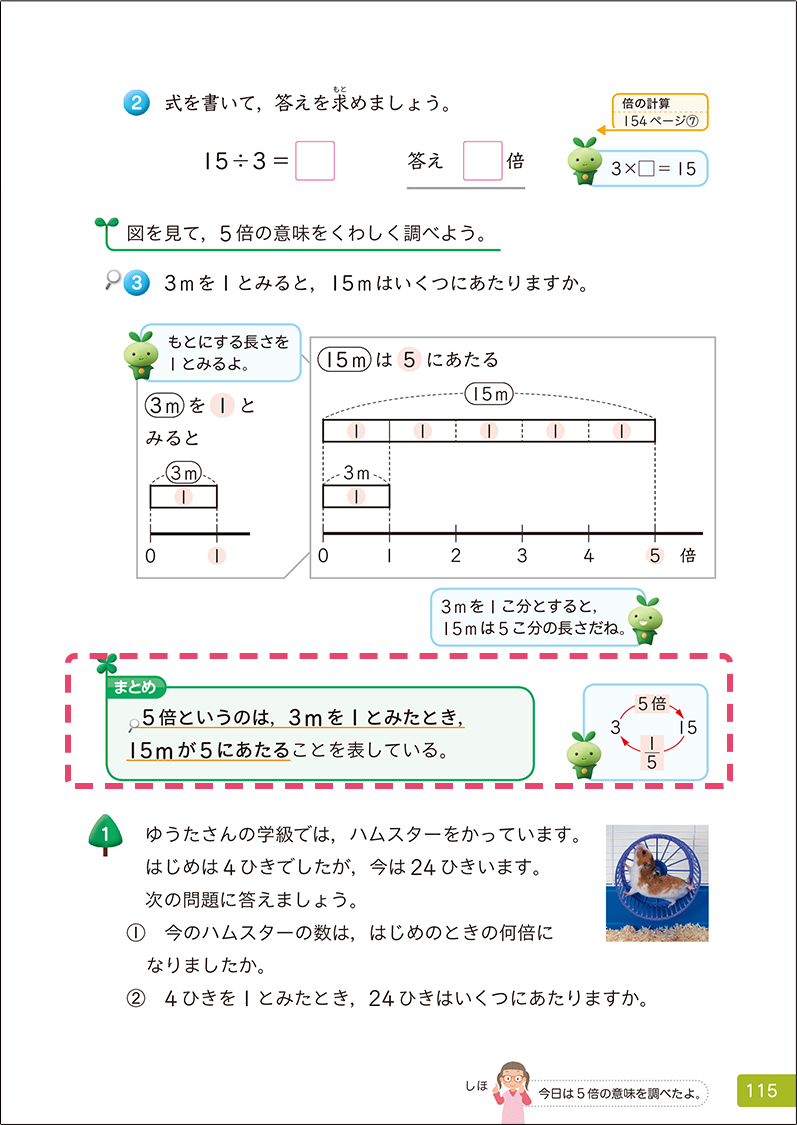
▼4年上「倍の見方」p.115
▼5年下「割合」p.67
